알고리즘 복잡도 표현 방법
이해하기 쉽고, 장황하지 않은 자료를 기반으로 강의를 진행합니다.
1. 알고리즘 복잡도 표현 방법¶
하나의 문제를 푸는 알고리즘은 다양할 수 있음¶
- 정수의 절대값은 정수값을 제곱한 값에 다시 루트를 씌우는 방식으로도 계산할 수 있음
여러 알고리즘 중에 어떤 알고리즘이 더 좋을까? - 알고리즘 분석¶
- 다양한 알고리즘 중 어느 알고리즘이 더 좋은지를 분석하는 것
- 시간 복잡도: 알고리즘 실행 속도
- 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈
반복문이 지배합니다.¶
- 예:
- 자동차로 서울에서 부산가기
- 자동차 문열기
- 자동차 문닫기
- 자동차 운전석 등받이 조정하기
- 자동차 시동걸기
- 자동차로 서울에서 부산가기
- 자동차 시동끄기
- 자동차 문열기
- 자동차 문닫기
- 자동차로 서울에서 부산가기
생각해보기
위 자동차 서울에서 부산가기에서 가장 총 시간에 영향을 많이 미칠 것 같은 요소는?
위 자동차 서울에서 부산가기에서 가장 총 시간에 영향을 많이 미칠 것 같은 요소는?
마찬가지로, 프로그래밍에서 시간 복잡도에 가장 영향을 많이 미치는 요소는 반복문¶
- 입력의 크기가 커지면 커질수록 반복문이 알고리즘 수행 시간을 지배함
알고리즘 성능 표기법¶
- O표기법은 알고리즘의 최악의 성능을 표시
- 가장 많이/일반적으로 사용함
- 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문
- Ω표기법은 알고리즘의 최고의 성능을 표시
- θ표기법은 정확한 알고리즘의 성능을 표시
대문자 O 표기법¶
- 빅 오 표기법이라고도 부름
- O(입력)
- 입력 n 에 따라 결정되는 시간 복잡도 함수
- O(1), O($log n$), O(n), O(n$log n$), O($n^2$), O($2^n$), O(n!)등으로 표기함
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음
- O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!)
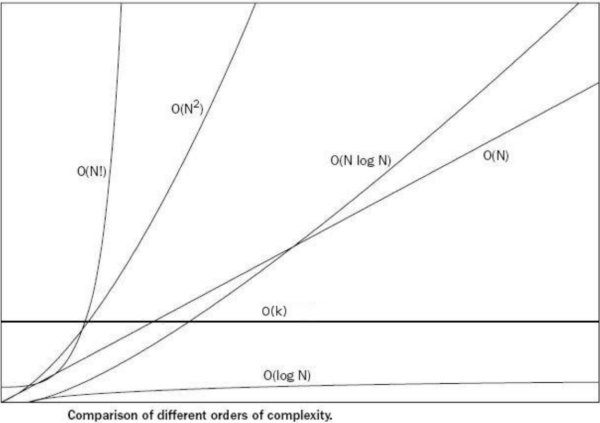
- 빅 오 입력값 표기 방법
- 예:
- 만약 시간 복잡도 함수가 2$n^2$ + 3n 이라면
- 가장 높은 차수는 2$n^2$
- 상수는 실제 큰 영향이 없음
- 결국 빅 오 표기법으로는 O($n^2$) (서울부터 부산까지 가는 자동차의 예를 상기)
- 만약 시간 복잡도 함수가 2$n^2$ + 3n 이라면
- 예:
프로그래밍 연습
1부터 n까지의 합을 구하는 알고리즘 작성해보기
1부터 n까지의 합을 구하는 알고리즘 작성해보기
In [56]:
def func(n):
count = 0
for num in range(1, n + 1):
count += num
return count
func(10)
Out[56]:
실제 알고리즘을 예로 각 알고리즘의 시간 복잡도와 빅 오 표기를 알아보자¶
알고리즘1: 1부터 n까지의 합을 구하는 알고리즘1¶
- 합을 기록할 변수를 만들고 0을 저장
- n을 1부터 1씩 증가하면서 반복
- 반복문 안에서 합을 기록할 변수에 1씩 증가된 값을 더함
- 반복이 끝나면 합을 출력
In [16]:
def sum_all(n):
total = 0
for num in range(1, n + 1):
total += num
return total
In [17]:
sum_all(100)
Out[17]:
알고리즘2: 1부터 n까지의 합을 구하는 알고리즘2¶
- $\frac { n (n + 1) }{ 2 }$
In [20]:
def sum_all(n):
return int(n * (n + 1) / 2)
In [21]:
sum_all(100)
Out[21]:
알고리즘1 시간 복잡도 구하기¶
- 1부터 n까지의 합을 구하는 알고리즘1
- 입력 n에 따라 덧셈을 n 번 해야 함 (반복문!)
- 그래서 빅 오 표기법으로는 시간 복잡도는 O(n)
- 1부터 n까지의 합을 구하는 알고리즘1
- 입력 n이 어떻든 간에, 곱셈/덧셈/나눗셈 하면 됨 (반복문이 없음!)
- 그래서 빅 오 표기법으로는 시간 복잡도는 O(1), 상수가 됨
알고리즘2: 리스트 데이터에서 동일한 이름을 가진 이름 추출하기¶
- set 사용하지 않고, 구현하기
In [29]:
names = ['Dave', 'David', 'Anthony', 'Andy', 'Dave']
프로그래밍 연습
이름을 리스트 데이터로 가진 리스트 변수를 넣으면, 해당 변수에서 동일한 이름을 가진 중복 리스트 데이터를 삭제한 리스트 출력하기
예:
### 참고 enumerate
- for index, name in enumerate(name_list):
- name_list 리스트 변수 길이 만큼 반복: 0 ~ (len(name_list) - 1)
- 이 때 index에는 인덱스번호가 0 ~ (len(name_list) - 1), name 에는 해당 인덱스 번호에 저장된 리스트 데이터가 저장됨
이름을 리스트 데이터로 가진 리스트 변수를 넣으면, 해당 변수에서 동일한 이름을 가진 중복 리스트 데이터를 삭제한 리스트 출력하기
예:
names = ['Dave', 'David', 'Anthony', 'David', 'Dave'] find_same_name(names) 출력: ['Dave', 'David', 'Anthony']
In [57]:
def find_same_name(name_list):
for index, name in enumerate(name_list): # 반복문에 주의!
for index2 in range(index + 1, len(name_list)): # 반복문에 주의!
if (name == name_list[index2]):
del name_list[index2]
return name_list
In [63]:
def find_same_name(name_list):
for index, name in enumerate(name_list):
for index2 in range(index + 1, len(name_list)):
if (name == name_list[index2]):
del name_list[index2]
return name_list
In [ ]:
In [64]:
name_list = ['Dave', 'David', 'Anthony', 'David', 'Dave']
find_same_name(name_list)
Out[64]:
알고리즘2 시간 복잡도 구하기¶
- 반복문이 중첩
- for name in name_list
- for index in range(name_index, len(name_list))
- 리스트 사이즈가 3 일때, (중복되는 이름이 없는 최악의 상황을 가정)
- 리스트 인덱스 0에 대해서는 1, 2 와 비교 (n - 1)
- 리스트 인덱스 1에 대해서는 2 와 비교 (n - 2)
- 결국 일반화 시키면, n (n - 1) / 2 --> $\frac { n^2}{ 2 } - \frac { n}{ 2 }$
- 여기서 가장 높은 차수만 빼고 상수와 나머지 차수를 다 제외 하면!
- $n^2$
- 그래서 빅 오 표기법으로는 시간 복잡도는 O($n^2$), 이 됨


