탐욕 알고리즘의 이해
이해하기 쉽고, 장황하지 않은 자료를 기반으로 강의를 진행합니다.
잔재미코딩 소식 공유
좀더 제약없이, IT 컨텐츠를 공유하고자, 자체 온라인 강의 사이트와 유투브 채널을
오픈하였습니다
응원해주시면, 곧 좋은 컨텐츠를 만들어서 공유하겠습니다
응원해주시면, 곧 좋은 컨텐츠를 만들어서 공유하겠습니다
● 잔재미코딩 유투브 오픈
[구독해보기]
4. 탐욕 알고리즘의 이해¶
1. 탐욕 알고리즘 이란?¶
- Greedy algorithm 또는 탐욕 알고리즘 이라고 불리움
- 최적의 해에 가까운 값을 구하기 위해 사용됨
- 여러 경우 중 하나를 결정해야할 때마다, 매순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행해서, 최종적인 값을 구하는 방식
In [5]:
coin_list = [1, 100, 50, 500]
print (coin_list)
coin_list.sort(reverse=True)
print (coin_list)
In [6]:
coin_list = [500, 100, 50, 1]
def min_coin_count(value, coin_list):
total_coin_count = 0
details = list()
coin_list.sort(reverse=True)
for coin in coin_list:
coin_num = value // coin
total_coin_count += coin_num
value -= coin_num * coin
details.append([coin, coin_num])
return total_coin_count, details
In [7]:
min_coin_count(4720, coin_list)
Out[7]:
본 자료와 같이 IT 기술을 잘 정리하여, 온라인 강의로 제공하고 있습니다
체계적으로 전문가 레벨까지 익힐 수 있도록 온라인 강의 로드맵을 제공합니다
문제2: 부분 배낭 문제 (Fractional Knapsack Problem)¶
- 무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣는 문제
- 각 물건은 무게(w)와 가치(v)로 표현될 수 있음
- 물건은 쪼갤 수 있으므로 물건의 일부분이 배낭에 넣어질 수 있음, 그래서 Fractional Knapsack Problem 으로 부름
- Fractional Knapsack Problem 의 반대로 물건을 쪼개서 넣을 수 없는 배낭 문제도 존재함 (0/1 Knapsack Problem 으로 부름)
In [13]:
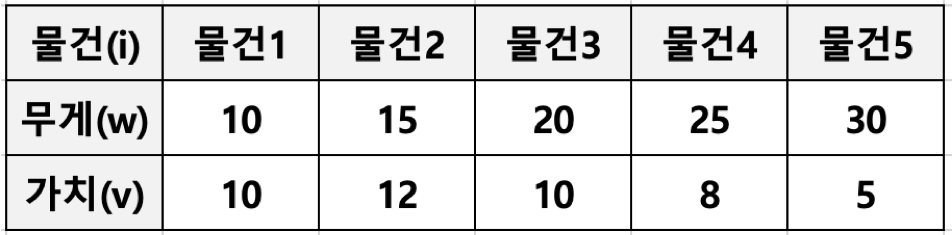
data_list = [(10, 10), (15, 12), (20, 10), (25, 8), (30, 5)]
In [19]:
def get_max_value(data_list, capacity):
data_list = sorted(data_list, key=lambda x: x[1] / x[0], reverse=True)
total_value = 0
details = list()
for data in data_list:
if capacity - data[0] >= 0:
capacity -= data[0]
total_value += data[1]
details.append([data[0], data[1], 1])
else:
fraction = capacity / data[0]
total_value += data[1] * fraction
details.append([data[0], data[1], fraction])
break
return total_value, details
In [20]:
get_max_value(data_list, 30)
Out[20]:
