잔재미코딩 강의
이해하기 쉽고, 장황하지 않은 자료를 기반으로 강의를 진행합니다.
3. Recursive Call (재귀 호출)¶
- 함수 안에서 동일한 함수를 호출하는 형태
- 여러 알고리즘 작성시 사용되므로, 익숙해져야 함
3.1 팩토리얼을 구하는 알고리즘을 Recursive Call 을 활용해서 알고리즘 작성하기¶
3.1.1. 간단한 경우부터 생각해보기¶
- 2! = 1 X 2
- 3! = 1 X 2 X 3
- 4! = 1 X 2 X 3 X 4
3.1.2. 규칙이 보임: n! = n X (n - 1)!¶
- 함수를 하나 만든다.
- 함수(n) 은 n > 1 이면 return n X 함수(n - 1)
- 함수(n) 은 n = 1 이면 return n
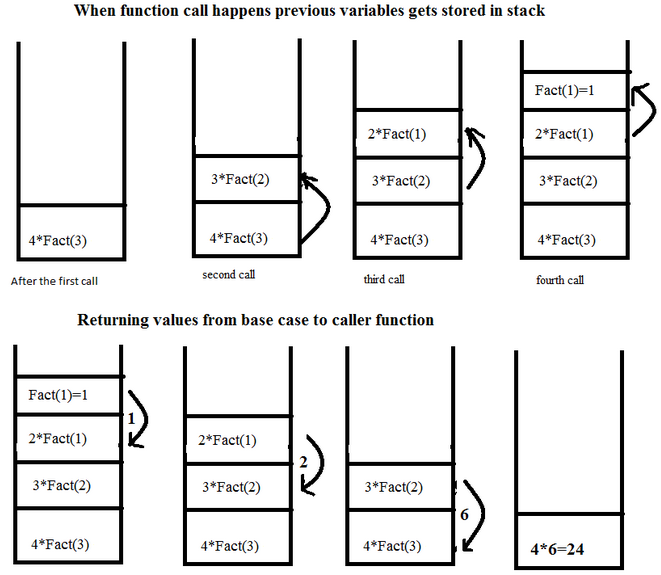
3.1.3. 검증 (코드로 검증하지 않고, 직접 간단한 경우부터 대입해서 검증해야 함)¶
- 먼저 2! 부터
- 함수(2) 이면, 2 > 1 이므로 2 X 함수(1)
- 함수(1) 은 1 이므로, return 2 X 1 = 2 맞다!
- 먼저 3! 부터
- 함수(3) 이면, 3 > 1 이므로 3 X 함수(2)
- 함수(2) 는 결국 1번에 의해 2! 이므로, return 2 X 1 = 2
- 3 X 함수(2) = 3 X 2 = 3 X 2 X 1 = 6 맞다!
- 먼저 4! 부터
- 함수(4) 이면, 4 > 1 이므로 4 X 함수(3)
- 함수(3) 은 결국 2번에 의해 3 X 2 X 1 = 6
- 4 X 함수(3) = 4 X 6 = 24 맞다!
3.1.4. 코드 레벨로 적어보기¶
In [67]:
# 3.1.2 항목에서 적어놓은 문장을 코드로 옮긴다. 필기에서는 좀더 코드레벨로 연습장에 적은 후에 작성
def factorial(num):
if num > 1:
return num * factorial(num - 1)
else:
return num
In [68]:
# 코드로 검증
for num in range(10):
print (factorial(num))
2.1.5. 알고리즘 시간 복잡도 구하기¶
- factorial(n) 은 n - 1 번의 factorial() 함수를 호출해서, 곱셈을 함 (일종의 n-1번 반복문을 호출한 것과 동일)
- O(n-1) 이므로 결국, O(n) (최상위 차수만 기재)
3.1. 예: 팩토리얼 구하기 (다시 코드보며 재귀 호출 예 이해하기)¶
In [ ]:
# factorial 함수 안에서 factorial 함수를 호출
def factorial(num):
if num > 1:
return num * factorial(num - 1)
else:
return num
재귀 호출의 일반적인 형태¶
In [ ]:
# 일반적인 형태1
def function(입력):
if 입력 > 일정값: # 입력이 일정 값 이상이면
return function(입력 - 1) # 입력보다 작은 값
else:
return 일정값 # 재귀 호출 종료
In [ ]:
# 일반적인 형태2
def function(입력):
if 입력 <= 일정값: # 입력이 일정 값보다 작으면
return 결과값 # 재귀 호출 종료
function(입력보다 작은 값)
return 결과값
In [71]:
# 일반적인 형태2 로 작성한 팩토리얼
def factorial(num):
if num <= 1:
return num
return_value = num * factorial(num - 1) # return num * factorial(num - 1) 로 작성하는 것도 좋음
return return_value
In [72]:
# 코드로 검증
for num in range(10):
print (factorial(num))
처음에는 재귀 호출이 이해가 가지 않으므로, 다음 코드를 실행하면서 이해하자¶
파이썬에서 재귀 함수는 깊이가(한번에 호출되는...) 1000회 이하가 되어야 함¶
프로그래밍 연습
다음 함수를 재귀 함수를 활용해서 완성해서 1부터 num까지의 곱이 출력되게 만드세요
다음 함수를 재귀 함수를 활용해서 완성해서 1부터 num까지의 곱이 출력되게 만드세요
def muliple(data):
if data <= 1:
return data
return -------------------------
multiple(10)
In [82]:
def multiple(data):
return_value = 1
for index in range(1, data+1):
return_value = return_value * index
return return_value
In [81]:
def multiple(data):
if data <= 1:
return data
return data * multiple(data - 1)
for num in range(10):
print (multiple(num))
프로그래밍 연습
숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요
숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요
참고: 임의 값으로 리스트 만들기 random.sample(0 ~ 99까지 중에서, 임의로 10개를 만들어서 10개 값을 가지는 리스트 변수 만들기 import random data = random.sample(range(100), 10)
In [83]:
import random
data = random.sample(range(100), 10)
data
Out[83]:
프로그래밍 연습
숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요 (재귀함수를 써보세요)
숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요 (재귀함수를 써보세요)
def sum_list(data):
if len(data) == 1:
return data[0]
return --------------------------------
import random
data = random.sample(range(100), 10)
print (sum_list(data))
In [89]:
def sum_list(data):
return_value = 0
for item in data:
return_value = return_value + item
return return_value
data_list = random.sample(range(100), 10)
sum_list(data_list)
Out[89]:
In [92]:
data_list
Out[92]:
In [94]:
data_list[-1]
Out[94]:
In [91]:
def sum_list(data):
# print(data)
if len(data) == 1:
return data[0]
return data[0] + sum_list(data[1:])
sum_list(data_list)
Out[91]:
프로그래밍 연습
회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함
회문을 판별할 수 있는 함수를 리스트 슬라이싱을 활용해서 만드세요
회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함
회문을 판별할 수 있는 함수를 리스트 슬라이싱을 활용해서 만드세요

참고 - 리스트 슬라이싱 string = 'Dave' string[-1] --> e string[0] --> D string[1:-1] --> av string[:-1] --> Dav
프로그래밍 연습
회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함
회문을 판별할 수 있는 함수를 재귀함수를 활용해서 만들어봅니다.
회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함
회문을 판별할 수 있는 함수를 재귀함수를 활용해서 만들어봅니다.
In [6]:
def recursive(string):
if len(string) == 1:
return True
if string[0] == string[-1]:
return recursive(string[1:-1])
else:
return False
print (recursive('rumur'))
In [100]:
def recursive(string):
if len(string) <= 1:
return True
if string[0] == string[-1]:
return recursive(string[1:-1])
else:
return False
print (recursive('abcdfdcba'))
협업 과제1(남에게 설명하면, 자신이 배운답니다.!)
다음 엑셀 파일에서 이름을 스페이스로 분리해서, 각 단어가 나온 횟수를 구해보세요
어떤 이름이나 성을 가진 사람이 많을지를 알기 위해, 새로운 쉬트에 단어가 나온 횟수가 높은 순으로 이름과 횟수를 정렬해서 넣어보세요
힌트: 문제를 잘라봅니다.
1. 각 이름을 스페이스로 짜르자
2. 각 이름을 사전에 key로 넣자
3. 이 때 사전에 이미 해당 key 가 있는지 확인하고, 해당 키가 있으면 value에 1을 더하고,
4. 해당 키가 없으면, value를 1로 해서 사전키를 만들면 될 것 같다.
다음 엑셀 파일에서 이름을 스페이스로 분리해서, 각 단어가 나온 횟수를 구해보세요
어떤 이름이나 성을 가진 사람이 많을지를 알기 위해, 새로운 쉬트에 단어가 나온 횟수가 높은 순으로 이름과 횟수를 정렬해서 넣어보세요
힌트: 문제를 잘라봅니다.
1. 각 이름을 스페이스로 짜르자
2. 각 이름을 사전에 key로 넣자
3. 이 때 사전에 이미 해당 key 가 있는지 확인하고, 해당 키가 있으면 value에 1을 더하고,
4. 해당 키가 없으면, value를 1로 해서 사전키를 만들면 될 것 같다.
이제 1번부터 하나씩 어떻게 할지 코드를 작성해보고, 1~4를 하나씩 해결해가자
참고: 문자열 짜르기
string = 'Dave Mr. Korea'
word_list = string.split(' ')
print (word_list)
In [143]:
import openpyxl
# 엑셀파일 열기
work_book = openpyxl.load_workbook('data/train.xlsx')
# 현재 Active Sheet 얻기
work_sheet = work_book.active
# Age Sorting 이라는 쉬트를 작성하는 예제
work_sheet_new = work_book.create_sheet('word sorting')
word_dict = dict()
for each_row in work_sheet.rows:
string = each_row[3].value
word_list = string.split()
for word in word_list:
if word in word_dict:
word_dict[word] += 1
else:
word_dict[word] = 1
sorted_word_list = sorted(word_dict, key=lambda k : word_dict[k], reverse=True)
for index, word in enumerate(sorted_word_list):
work_sheet_new.cell(row=index + 1, column=1).value = word
work_sheet_new.cell(row=index + 1, column=2).value = word_dict[word]
# 엑셀 파일 저장
work_book.save("score8.xlsx")
work_book.close()
협업 과제2(남에게 설명하면, 자신이 배운답니다.!)
1, 정수 n에 대해 2. n이 홀수이면 3 X n + 1 을 하고, 3. n이 짝수이면 n 을 2로 나눕니다. 4. 이렇게 계속 진행해서 n 이 결국 1이 될 때까지 2와 3의 과정을 반복합니다.
1, 정수 n에 대해 2. n이 홀수이면 3 X n + 1 을 하고, 3. n이 짝수이면 n 을 2로 나눕니다. 4. 이렇게 계속 진행해서 n 이 결국 1이 될 때까지 2와 3의 과정을 반복합니다.
예를 들어 n에 3을 넣으면,
3 10 5 16 8 4 2 1
이 됩니다.
이렇게 정수 n을 입력받아, 위 알고리즘에 의해 1이 되는 과정을 모두 출력하는 함수를 작성하세요.
In [37]:
def func(data):
print (data)
if data == 1:
return
if data % 2 == 0:
return func(int(data / 2))
else:
return func(3 * data + 1)
3.2. 최대 공약수 구하기¶
- 두 정수를 입력받아서, 두 정수의 최대 공약수를 출력해주는 알고리즘 작성하기
- 두 정수는 0 보다 크고, 100 이하인 수
3.2.1 입력과 출력, 조건 확인이 우선!¶
- 입력: 두 정수 num1, num2
- 0 < num1 <= 100, 0 < num2 <= 100
- 출력: 두 정수(num1, num2)의 최대 공약수
3.2.2 문제 이해¶
- 최대공약수: 두 수의 공통된 약수 중에서, 가장 큰 값
- 약수: 어떤 정수를 나머지 없이 나눌 수 있는 정수
3.2.3 최대한 간단한 예로 규칙 생각해보기¶
- 2와 4의 최대공약수: 2 (2%2, 4%2 는 0)
- 3과 6의 최대공약수: 3 (3%3, 6%3 은 0)
- 4와 6의 최대공약수
- 4%4 = 0, 6%4 = 2
- 4%3 = 3
- 4%2 = 0, 6%2 = 0
3.2.4 알고리즘¶
- 두 입력된 정수 중, 적은 수로 두 정수의 나머지를 구한다.
- 둘 다 나머지가 0이면 해당 값 리턴
- 그렇지 않으면, 적은 수 - 1 로 다시 두 정수의 나머지를 구한다.
3.2.5 고안한 규칙으로 다시 검증 (절대 코드를 먼저 작성하고, 바로 테스트해보지 않습니다.)¶
- 2와 4의 최대공약수: 2 (2%2, 4%2 는 0)
- 3과 6의 최대공약수: 3 (3%3, 6%3 은 0)
- 4와 6의 최대공약수
- 4%4 = 0, 6%4 = 2
- 4%3 = 3
- 4%2 = 0, 6%2 = 0
3.2.6 코드 작성하기 (빈칸 채우기 프로그래밍 연습!)¶
In [45]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(----------------):
if --------------------------------------:
return divisor
In [105]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(divisor, 0, -1):
if num1 % divisor == 0 and num2 % divisor == 0:
return divisor
return 1
In [118]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(divisor, 0, -1):
if (num1 % index == 0) and (num2 % index == 0):
return index
return 1
In [119]:
gcd(100, 15)
Out[119]:
3.2.7 코드 refinement (코드를 견고하게 만들기)¶
In [34]:
# 코드 refinement
def gcd(num1, num2):
if type(num1) is not int: # 조건1: num1과 num2이 정수인지!
return 0
if type(num2) is not int:
return 0
if num1 < 1 or num1 > 100: # 조건2: 0 < num1 <= 100, 0 < num2 <= 100
return 0
if num2 < 1 or num2 > 100:
return 0
if num1 > num2:
divisor = num2
else:
divisor = num1
for sub_divisor in range(divisor, 1, -1): # 10 ~ 1까지 테스트하면, 1일 때 불필요하게 나머지를 구하게 됨, 10 ~ 2까지로!
if num1 % sub_divisor == 0 and num2 % sub_divisor == 0:
return sub_divisor
return 1
In [41]:
# 테스트 입력 넣어보기
# result = gcd(20.0, 15)
# result = gcd(101, 15)
result = gcd(20, 15)
if result == 0:
print ("입력에 문제가 있습니다.")
else:
print ("최대 공약수는 " + str(result) + " 입니다.")
3.2.8 다른 알고리즘 (유클리드(Euclid) 알고리즘)¶
a와 b의 최대 공약수는 b와 a % b (a를 b로 나눈 나머지, b가 a보다 적은 수)의 최대 공약수와 같음¶
규칙 검증¶
- 30, 20의 최대 공약수는 20과 30 % 20, 즉 20과 10의 최대공약수와 같음
- 20, 10의 최대 공약수는 10과 20 % 10, 즉 0이므로, 10이 최대 공약수
- 48, 12의 최대 공약수는 12와 48 % 12, 즉 0이므로, 12가 최대 공약수
- 48, 18의 최대 공약수는 18와 48 % 18, 즉 12이므로, 다시 18과 18 % 12, 즉 6이므로, 다시 12와 12 % 6, 즉 0이므로 6이 최대 공약수
알고리즘 (재귀 함수 활용)¶
- 두 수, a, b를 입력받고, a와 b 중 적은 수를 알아냄
- 둘 중의 하나가 0 이면, 나머지 하나를 리턴값으로 리턴
- 그렇지 않으면, b 와 a % b 로 다시 계산 (재귀 함수)
프로그래밍 연습: 빈칸 채우기¶
In [65]:
def gcd2(a, b):
while b > 1:
if -----------------------:
break
else:
-----------------------
a = b
b = temp
return b
In [67]:
gcd2(48, 12)
Out[67]:
프로그래밍 연습
위 문제를 재귀함수를 써서 풀어보기
위 문제를 재귀함수를 써서 풀어보기
In [120]:
def gcd2(a, b):
if a == 0:
return b
elif b == 0:
return a
return gcd2(b, a % b)
In [70]:
def gcd2(a, b):
if a == 0:
------------
elif b == 0:
------------
return --------------------
In [123]:
gcd2(5, 15)
Out[123]:
In [122]:
gcd2(15, 5)
Out[122]:
빅 오 표기법으로 정확히 명시되기는 어렵지만, 3.2.7 알고리즘이 3.2.5 알고리즘보다 계산 횟수가 적음¶
프로그래밍 연습
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
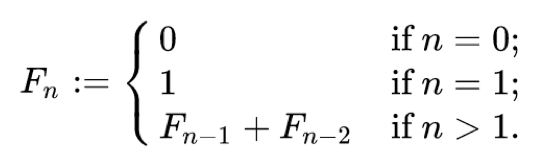
함수를 fibo 라고 하면, fibo(0):0 fibo(1):1 fibo(2):1 fibo(3):2 fibo(4):3 fibo(5):5 fibo(6):8 fibo(7):13 fibo(8):21 fibo(9):34
In [86]:
def fibo(num):
if num == 0 or num == 1:
return num
return fibo(num - 1) + fibo(num - 2)
In [124]:
def fibo(num):
if num == 0:
return 0
elif num == 1:
return 1
return fibo(num - 1) + fibo(num - 2)
In [125]:
for num in range(10):
print ('fibo(' + str(num) + '):' + str(fibo(num)))
3.3. 하노이탑 문제 (초심화)¶
- 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판이 있음
- 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있음

- 다음 조건을 따라서, n개의 원판을 다른 기둥으로 최소 몇 번 옮겨야 하는지, 횟수를 출력하는 문제
- 한 번에 하나의 원판만 옮길 수 있음
- 큰 원판이 작은 원판 위에 있어서는 안 됨
- 출처: 위키 백과 (https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91)
3.3.1. 작은 경우부터 생각해보기 (1개일 때는 한번에 이동 가능, 2개일 때는 3번에 이동 가능)¶
- 다음은 3개 일 때: 7번으로 이동 가능
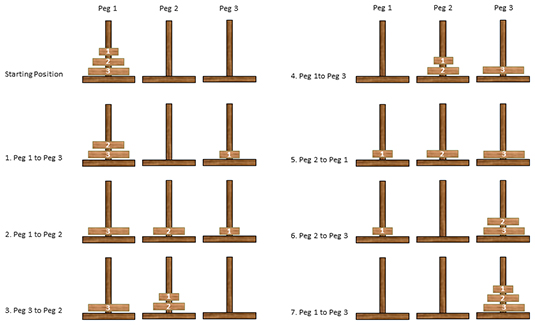
- 다음 코드 실행해서 하노이탑 생각해보기 (다음 코드 실행이 안되면, 링크로 직접 접속 http://www.novelgames.com/ko/tower/ )
In [126]:
%%html
<script async src="//license.novelgames.com/games/game.js"></script>
<ins class="novelgames_cloudgame"
data-game-short-name="tower"
data-language="ko"
></ins>
3.3.2. 원반이 n 개일 때 첫번째 기둥에서 세번째 기둥으로 옮기는 방법 (일반화)¶
- 원반 n - 1 개를 두번째 기둥으로 옮긴 후
- 첫번째 기둥의 가장 큰 원반을 세번째 기둥으로 옮기고,
- 두번째 기둥의 n - 1 개 원반을 세번째 기둥으로 옮기면 됨
3.3.3. 규칙¶
- 원반이 한 개이면 첫 번째 기둥에서 세 번째 기둥으로 바로 옮김
- 원반이 n 개이면
- 첫 번째 기둥에 있는 n - 1개를 세 번째 기둥을 활용해서 두 번째 기둥으로 옮김
- 첫 번째 기둥에 있는 가장 큰 원반을 세 번째 기둥으로 옮김
- 두 번째 기둥에 있는 n - 1개를 첫 번째 기둥을 활용해서 세 번째 기둥으로 옮김
3.3.4. 그대로 코드로 옮겨보자 (재귀 호출 활용)¶
In [96]:
# first point: 현재 있는 기둥 (첫번째 기둥)
# second point: 활용하는 기둥 (두번째 기둥)
# third point: 옮기려는 기둥 (세번째 기둥)
# hanoi(n, 현재 있는 기둥, 활용하는 기둥, 옮기려는 기둥)
# hanoi(n) 원반 n개에 대해 첫 번째 기둥에 있는 원반을 두 번째 기둥을 활용해서, 세 번째 기둥으로 옮기는 방법을 출력하는 함수
def hanoi(n, first='첫번째기둥', second='두번째기둥', third='세번째기둥'):
if n == 1:
print(str(n), first, "->", third)
return
hanoi(n-1, first, third, second)
print(str(n), first, "->", third)
hanoi(n-1, second, first, third)
In [97]:
hanoi(1)
In [98]:
hanoi(2)
In [99]:
hanoi(3)
In [100]:
hanoi(4)
3.3.5. 알고리즘 분석¶
- n = 1 일 때, 1
- n = 2 일 때, 3
- n = 3 일 때, 7
- n = 4 일 때, 15
- n 일 때, $2^n - 1$, 즉 시간 복잡도는 O($2^n$)
도전 과제
연습 과제는 그냥 과제와 달리, 난이도가 매우 높을 때도 있습니다. 한번에 못푸는 것이 당연한 문제!, 여러번 풀이보고, 다시 스스로 풀어보면서 연습하는 문제임
연습 과제는 그냥 과제와 달리, 난이도가 매우 높을 때도 있습니다. 한번에 못푸는 것이 당연한 문제!, 여러번 풀이보고, 다시 스스로 풀어보면서 연습하는 문제임
문제: 정수 4를 1, 2, 3의 조합으로 나타내는 방법은 다음과 같이 총 7가지가 있음 1+1+1+1 1+1+2 1+2+1 2+1+1 2+2 1+3 3+1 정수 n이 입력으로 주어졌을 때, n을 1, 2, 3의 합으로 나타낼 수 있는 방법의 수를 구하시오
힌트: 정수 n을 만들 수 있는 경우의 수를 리턴하는 함수를 f(n) 이라고 하면,
f(n)은 f(n-1) + f(n-2) + f(n-3) 과 동일하다는 패턴 찾기
출처: ACM-ICPC > Regionals > Asia > Korea > Asia Regional - Taejon 2001
In [104]:
def f(data):
if data < 0:
return 0
if data == 0:
return 1
elif data == 1:
return 1
elif data == 2:
return 2
elif data == 3:
return 4
return f(data - 1) + f(data - 2) + f(data - 3)
In [94]:
def is_palindrome(string):
if len(string) < 2:
return True
if string[0] != string[-1]:
return False
return is_palindrome(string[1:-1])
In [37]:
def func(data):
print (data)
if data == 1:
return
if data % 2 == 0:
return func(int(data / 2))
else:
return func(3 * data + 1)
3.2. 최대 공약수 구하기¶
- 두 정수를 입력받아서, 두 정수의 최대 공약수를 출력해주는 알고리즘 작성하기
- 두 정수는 0 보다 크고, 100 이하인 수
3.2.1 입력과 출력, 조건 확인이 우선!¶
- 입력: 두 정수 num1, num2
- 0 < num1 <= 100, 0 < num2 <= 100
- 출력: 두 정수(num1, num2)의 최대 공약수
3.2.2 문제 이해¶
- 최대공약수: 두 수의 공통된 약수 중에서, 가장 큰 값
- 약수: 어떤 정수를 나머지 없이 나눌 수 있는 정수
3.2.3 최대한 간단한 예로 규칙 생각해보기¶
- 2와 4의 최대공약수: 2 (2%2, 4%2 는 0)
- 3과 6의 최대공약수: 3 (3%3, 6%3 은 0)
- 4와 6의 최대공약수
- 4%4 = 0, 6%4 = 2
- 4%3 = 3
- 4%2 = 0, 6%2 = 0
3.2.4 알고리즘¶
- 두 입력된 정수 중, 적은 수로 두 정수의 나머지를 구한다.
- 둘 다 나머지가 0이면 해당 값 리턴
- 그렇지 않으면, 적은 수 - 1 로 다시 두 정수의 나머지를 구한다.
3.2.5 고안한 규칙으로 다시 검증 (절대 코드를 먼저 작성하고, 바로 테스트해보지 않습니다.)¶
- 2와 4의 최대공약수: 2 (2%2, 4%2 는 0)
- 3과 6의 최대공약수: 3 (3%3, 6%3 은 0)
- 4와 6의 최대공약수
- 4%4 = 0, 6%4 = 2
- 4%3 = 3
- 4%2 = 0, 6%2 = 0
3.2.6 코드 작성하기 (빈칸 채우기 프로그래밍 연습!)¶
In [45]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(----------------):
if --------------------------------------:
return divisor
In [105]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(divisor, 0, -1):
if num1 % divisor == 0 and num2 % divisor == 0:
return divisor
return 1
In [118]:
def gcd(num1, num2):
if num1 > num2:
divisor = num2
else:
divisor = num1
for index in range(divisor, 0, -1):
if (num1 % index == 0) and (num2 % index == 0):
return index
return 1
In [119]:
gcd(100, 15)
Out[119]:
3.2.7 코드 refinement (코드를 견고하게 만들기)¶
In [34]:
# 코드 refinement
def gcd(num1, num2):
if type(num1) is not int: # 조건1: num1과 num2이 정수인지!
return 0
if type(num2) is not int:
return 0
if num1 < 1 or num1 > 100: # 조건2: 0 < num1 <= 100, 0 < num2 <= 100
return 0
if num2 < 1 or num2 > 100:
return 0
if num1 > num2:
divisor = num2
else:
divisor = num1
for sub_divisor in range(divisor, 1, -1): # 10 ~ 1까지 테스트하면, 1일 때 불필요하게 나머지를 구하게 됨, 10 ~ 2까지로!
if num1 % sub_divisor == 0 and num2 % sub_divisor == 0:
return sub_divisor
return 1
In [41]:
# 테스트 입력 넣어보기
# result = gcd(20.0, 15)
# result = gcd(101, 15)
result = gcd(20, 15)
if result == 0:
print ("입력에 문제가 있습니다.")
else:
print ("최대 공약수는 " + str(result) + " 입니다.")
3.2.8 다른 알고리즘 (유클리드(Euclid) 알고리즘)¶
a와 b의 최대 공약수는 b와 a % b (a를 b로 나눈 나머지, b가 a보다 적은 수)의 최대 공약수와 같음¶
규칙 검증¶
- 30, 20의 최대 공약수는 20과 30 % 20, 즉 20과 10의 최대공약수와 같음
- 20, 10의 최대 공약수는 10과 20 % 10, 즉 0이므로, 10이 최대 공약수
- 48, 12의 최대 공약수는 12와 48 % 12, 즉 0이므로, 12가 최대 공약수
- 48, 18의 최대 공약수는 18와 48 % 18, 즉 12이므로, 다시 18과 18 % 12, 즉 6이므로, 다시 12와 12 % 6, 즉 0이므로 6이 최대 공약수
알고리즘 (재귀 함수 활용)¶
- 두 수, a, b를 입력받고, a와 b 중 적은 수를 알아냄
- 둘 중의 하나가 0 이면, 나머지 하나를 리턴값으로 리턴
- 그렇지 않으면, b 와 a % b 로 다시 계산 (재귀 함수)
프로그래밍 연습: 빈칸 채우기¶
In [65]:
def gcd2(a, b):
while b > 1:
if -----------------------:
break
else:
-----------------------
a = b
b = temp
return b
In [67]:
gcd2(48, 12)
Out[67]:
프로그래밍 연습
위 문제를 재귀함수를 써서 풀어보기
위 문제를 재귀함수를 써서 풀어보기
In [120]:
def gcd2(a, b):
if a == 0:
return b
elif b == 0:
return a
return gcd2(b, a % b)
In [70]:
def gcd2(a, b):
if a == 0:
------------
elif b == 0:
------------
return --------------------
In [123]:
gcd2(5, 15)
Out[123]:
In [122]:
gcd2(15, 5)
Out[122]:
빅 오 표기법으로 정확히 명시되기는 어렵지만, 3.2.7 알고리즘이 3.2.5 알고리즘보다 계산 횟수가 적음¶
프로그래밍 연습
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
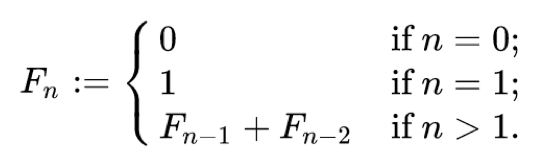
함수를 fibo 라고 하면, fibo(0):0 fibo(1):1 fibo(2):1 fibo(3):2 fibo(4):3 fibo(5):5 fibo(6):8 fibo(7):13 fibo(8):21 fibo(9):34
In [86]:
def fibo(num):
if num == 0 or num == 1:
return num
return fibo(num - 1) + fibo(num - 2)
In [124]:
def fibo(num):
if num == 0:
return 0
elif num == 1:
return 1
return fibo(num - 1) + fibo(num - 2)
In [125]:
for num in range(10):
print ('fibo(' + str(num) + '):' + str(fibo(num)))
3.3. 하노이탑 문제 (초심화)¶
- 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판이 있음
- 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있음

- 다음 조건을 따라서, n개의 원판을 다른 기둥으로 최소 몇 번 옮겨야 하는지, 횟수를 출력하는 문제
- 한 번에 하나의 원판만 옮길 수 있음
- 큰 원판이 작은 원판 위에 있어서는 안 됨
- 출처: 위키 백과 (https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91)
3.3.1. 작은 경우부터 생각해보기 (1개일 때는 한번에 이동 가능, 2개일 때는 3번에 이동 가능)¶
- 다음은 3개 일 때: 7번으로 이동 가능

- 다음 코드 실행해서 하노이탑 생각해보기 (다음 코드 실행이 안되면, 링크로 직접 접속 http://www.novelgames.com/ko/tower/ )
In [126]:
%%html
<script async src="//license.novelgames.com/games/game.js"></script>
<ins class="novelgames_cloudgame"
data-game-short-name="tower"
data-language="ko"
></ins>
3.3.2. 원반이 n 개일 때 첫번째 기둥에서 세번째 기둥으로 옮기는 방법 (일반화)¶
- 원반 n - 1 개를 두번째 기둥으로 옮긴 후
- 첫번째 기둥의 가장 큰 원반을 세번째 기둥으로 옮기고,
- 두번째 기둥의 n - 1 개 원반을 세번째 기둥으로 옮기면 됨
3.3.3. 규칙¶
- 원반이 한 개이면 첫 번째 기둥에서 세 번째 기둥으로 바로 옮김
- 원반이 n 개이면
- 첫 번째 기둥에 있는 n - 1개를 세 번째 기둥을 활용해서 두 번째 기둥으로 옮김
- 첫 번째 기둥에 있는 가장 큰 원반을 세 번째 기둥으로 옮김
- 두 번째 기둥에 있는 n - 1개를 첫 번째 기둥을 활용해서 세 번째 기둥으로 옮김
3.3.4. 그대로 코드로 옮겨보자 (재귀 호출 활용)¶
In [96]:
# first point: 현재 있는 기둥 (첫번째 기둥)
# second point: 활용하는 기둥 (두번째 기둥)
# third point: 옮기려는 기둥 (세번째 기둥)
# hanoi(n, 현재 있는 기둥, 활용하는 기둥, 옮기려는 기둥)
# hanoi(n) 원반 n개에 대해 첫 번째 기둥에 있는 원반을 두 번째 기둥을 활용해서, 세 번째 기둥으로 옮기는 방법을 출력하는 함수
def hanoi(n, first='첫번째기둥', second='두번째기둥', third='세번째기둥'):
if n == 1:
print(str(n), first, "->", third)
return
hanoi(n-1, first, third, second)
print(str(n), first, "->", third)
hanoi(n-1, second, first, third)
In [97]:
hanoi(1)
In [98]:
hanoi(2)
In [99]:
hanoi(3)
In [100]:
hanoi(4)
3.3.5. 알고리즘 분석¶
- n = 1 일 때, 1
- n = 2 일 때, 3
- n = 3 일 때, 7
- n = 4 일 때, 15
- n 일 때, $2^n - 1$, 즉 시간 복잡도는 O($2^n$)
도전 과제
연습 과제는 그냥 과제와 달리, 난이도가 매우 높을 때도 있습니다. 한번에 못푸는 것이 당연한 문제!, 여러번 풀이보고, 다시 스스로 풀어보면서 연습하는 문제임
연습 과제는 그냥 과제와 달리, 난이도가 매우 높을 때도 있습니다. 한번에 못푸는 것이 당연한 문제!, 여러번 풀이보고, 다시 스스로 풀어보면서 연습하는 문제임
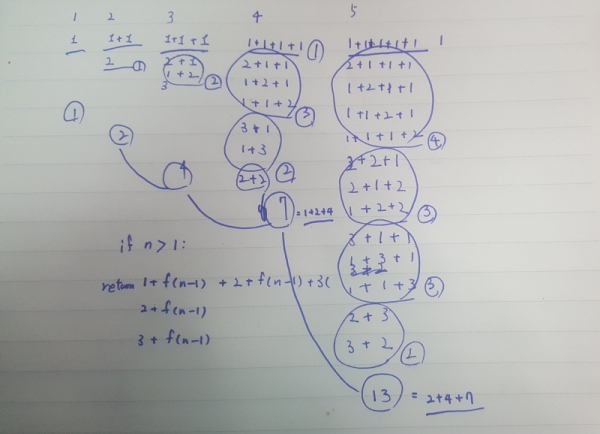
문제: 정수 4를 1, 2, 3의 조합으로 나타내는 방법은 다음과 같이 총 7가지가 있음 1+1+1+1 1+1+2 1+2+1 2+1+1 2+2 1+3 3+1 정수 n이 입력으로 주어졌을 때, n을 1, 2, 3의 합으로 나타낼 수 있는 방법의 수를 구하시오
힌트: 정수 n을 만들 수 있는 경우의 수를 리턴하는 함수를 f(n) 이라고 하면,
f(n)은 f(n-1) + f(n-2) + f(n-3) 과 동일하다는 패턴 찾기
출처: ACM-ICPC > Regionals > Asia > Korea > Asia Regional - Taejon 2001
In [104]:
def f(data):
if data < 0:
return 0
if data == 0:
return 1
elif data == 1:
return 1
elif data == 2:
return 2
elif data == 3:
return 4
return f(data - 1) + f(data - 2) + f(data - 3)

In [94]:
def is_palindrome(string):
if len(string) < 2:
return True
if string[0] != string[-1]:
return False
return is_palindrome(string[1:-1])